Mixed problems¶
The pymoo interface supports the solution of mixed integer/float problems via the genetic algorithm MixedVariableGA. Here we demonstrate this by maximizing the number if points that fit inside a circle and lie on a regular grid.
These are the imports:
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from iwopy import Problem, Objective
from iwopy.interfaces.pymoo import Optimizer_pymoo
The problem describes points on a regular grid of size nx * ny. Points that lie outside of the given radius will be marked by a False value in a boolean array called valid:
In [2]:
class GridProblem(Problem):
def __init__(self, n_row_max, radius, min_dist, ctol=1e-3):
super().__init__(name="grid_problem")
self.n_row_max = n_row_max
self.radius = float(radius)
self.min_dist = float(min_dist)
self.max_dist = 2*radius
self.xy = None
self.valid = None
def initialize(self, verbosity=1):
super().initialize(verbosity)
self.apply_individual(self.initial_values_int(), self.initial_values_float())
def var_names_int(self):
return ["nx", "ny"]
def initial_values_int(self):
return [2, 2]
def min_values_int(self):
return [1, 1]
def max_values_int(self):
return [self.n_row_max, self.n_row_max]
def var_names_float(self):
return ["x0", "y0", "dx", "dy", "alpha"]
def initial_values_float(self):
return [0., 0., self.min_dist, self.min_dist, 0.]
def min_values_float(self):
return [-2*self.radius, -2*self.radius, self.min_dist, self.min_dist, 0.]
def max_values_float(self):
return [self.radius, self.radius, self.max_dist, self.max_dist, 90.]
def apply_individual(self, vars_int, vars_float):
""" Create points on a regular grid, and evaluate their validity """
nx, ny = vars_int
x0, y0, dx, dy, alpha = vars_float
a = np.deg2rad(alpha)
nax = np.array([np.cos(a), np.sin(a), 0.])
naz = np.array([0., 0., 1.])
nay = np.cross(naz, nax)
self.xy = np.zeros((nx, ny, 2))
self.xy[:] = np.array([x0, y0])[None, None, :]
self.xy[:] += np.arange(nx)[:, None, None] * dx * nax[None, None, :2]
self.xy[:] += np.arange(ny)[None, :, None] * dy * nay[None, None, :2]
self.valid = np.linalg.norm(self.xy, axis=-1) <= self.radius
return self.xy, self.valid
def apply_population(self, vars_int, vars_float):
""" Create points on a regular grid, and evaluate their validity """
n_pop = vars_int.shape[0]
nx = vars_int[:, 0]
ny = vars_int[:, 1]
x0 = vars_float[:, 0]
y0 = vars_float[:, 1]
dx = vars_float[:, 2]
dy = vars_float[:, 3]
alpha = vars_float[:, 4]
a = np.deg2rad(alpha)
nax = np.stack([np.cos(a), np.sin(a), np.zeros(a.shape)], axis=-1)
naz = np.zeros_like(nax)
naz[:, 2] = 1
nay = np.cross(naz, nax)
mx = np.max(nx)
my = np.max(ny)
self.xy = np.full((n_pop, mx, my, 2), -2*self.radius)
for i in range(n_pop):
self.xy[i, :nx[i], :ny[i]] = np.array([x0[i], y0[i]])[None, None, :]
self.xy[i, :nx[i], :ny[i]] += np.arange(nx[i])[:, None, None] * dx[i, None, None, None] * nax[i, None, None, :2]
self.xy[i, :nx[i], :ny[i]] += np.arange(ny[i])[None, :, None] * dy[i, None, None, None] * nay[i, None, None, :2]
self.valid = np.linalg.norm(self.xy, axis=-1) <= self.radius
return self.xy, self.valid
def get_fig(self, xy=None, valid=None):
if xy is None:
xy = self.xy
if valid is None:
valid = self.valid
nx, ny = xy.shape[:2]
xy = xy.reshape(nx*ny, 2)[valid.reshape(nx*ny)]
fig, ax = plt.subplots()
ax.scatter(xy[:, 0], xy[:, 1], color="orange")
ax.add_patch(plt.Circle((0, 0), self.radius, color="darkred", fill=False))
ax.set_aspect("equal", adjustable="box")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title(f"N = {len(xy)}, min_dist = {self.min_dist}")
return fig
Notice that the calculate_individual and calculate_population functions return the current grid points and the validity array. This problem has two integer variables nx and ny, determining the number of grid points in x and y directions, respectively, and 5 float type variables.
Our objective is the maximization of the total number of points within the circle:
In [3]:
class MaxN(Objective):
def __init__(self, problem):
super().__init__(problem, "maxN", vnames_int=problem.var_names_int(),
vnames_float=problem.var_names_float())
def n_components(self):
return 1
def maximize(self):
return [True]
def calc_individual(self, vars_int, vars_float, problem_results, cmpnts=None):
xy, valid = problem_results
return np.sum(valid)
def calc_population(self, vars_int, vars_float, problem_results, cmpnts=None):
xy, valid = problem_results
return np.sum(valid, axis=(1, 2))[:, None]
This objective makes use of the returned validity array. We can now solve this with the appropriate algorithm from pymoo:
In [4]:
problem = GridProblem(n_row_max=1000, radius=5, min_dist=0.5)
problem.add_objective(MaxN(problem))
problem.initialize()
Problem 'grid_problem' (GridProblem): Initializing
--------------------------------------------------
n_vars_int : 2
n_vars_float : 5
--------------------------------------------------
n_objectives : 1
n_obj_cmptns : 1
--------------------------------------------------
n_constraints: 0
n_con_cmptns : 0
--------------------------------------------------
In [5]:
solver = Optimizer_pymoo(
problem,
problem_pars=dict(
vectorize=True,
),
algo_pars=dict(
type="MixedVariableGA",
pop_size=40,
seed=42,
),
setup_pars=dict(
),
term_pars=('n_eval', 1000),
)
solver.initialize()
solver.print_info()
Initializing Optimizer_pymoo
Selecting algorithm: MixedVariableGA (MixedVariableGA)
Problem:
--------
vectorize: True
Algorithm:
----------
type: MixedVariableGA
pop_size: 40
seed: 42
Termination:
------------
n_eval: 1000
Here tol is an IPOPT parameter that defines the convergence tolerance. Now we are finally ready - let’s solve the problem!
In [6]:
results = solver.solve()
solver.finalize(results)
=================================================
n_gen | n_eval | f_avg | f_min
=================================================
1 | 40 | -3.100000E+00 | -1.800000E+01
2 | 80 | -5.425000E+00 | -2.400000E+01
3 | 120 | -1.132500E+01 | -5.100000E+01
4 | 160 | -2.195000E+01 | -6.800000E+01
5 | 200 | -3.755000E+01 | -1.120000E+02
6 | 240 | -6.500000E+01 | -1.530000E+02
7 | 280 | -9.782500E+01 | -1.710000E+02
8 | 320 | -1.257500E+02 | -2.590000E+02
9 | 360 | -1.531750E+02 | -2.590000E+02
10 | 400 | -1.788000E+02 | -2.680000E+02
11 | 440 | -2.088500E+02 | -2.740000E+02
12 | 480 | -2.367500E+02 | -2.750000E+02
13 | 520 | -2.557750E+02 | -2.750000E+02
14 | 560 | -2.630750E+02 | -2.800000E+02
15 | 600 | -2.696000E+02 | -3.120000E+02
16 | 640 | -2.793250E+02 | -3.120000E+02
17 | 680 | -2.868250E+02 | -3.120000E+02
18 | 720 | -2.933250E+02 | -3.120000E+02
19 | 760 | -2.991250E+02 | -3.120000E+02
20 | 800 | -3.042500E+02 | -3.150000E+02
21 | 840 | -3.078500E+02 | -3.150000E+02
22 | 880 | -3.110000E+02 | -3.150000E+02
23 | 920 | -3.125500E+02 | -3.150000E+02
24 | 960 | -3.135250E+02 | -3.160000E+02
25 | 1000 | -3.140250E+02 | -3.160000E+02
Optimizer_pymoo: Optimization run finished
Success: True
Best maxN = 316.0
These are the results:
In [7]:
print(results)
fig = problem.get_fig()
plt.show()
plt.close(fig)
Results problem 'grid_problem':
--------------------------------
Integer variables:
0: nx = 721
1: ny = 337
--------------------------------
Float variables:
0: x0 = -9.852999e+00
1: y0 = -8.461444e+00
2: dx = 5.024268e-01
3: dy = 5.000655e-01
4: alpha = 6.319982e+00
--------------------------------
Objectives:
0: maxN = 3.160000e+02
--------------------------------
Success: True
--------------------------------
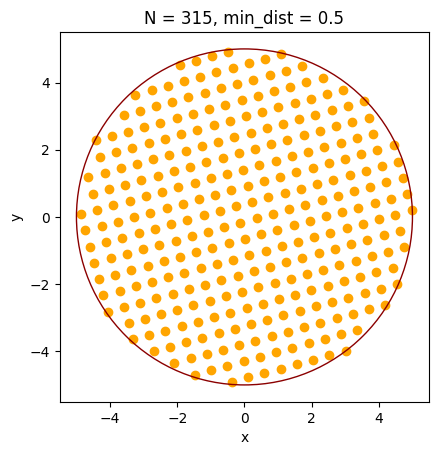
Clearly the circle is fully filled with points on a regular grid.