Wake steering¶

This example demonstrates how to optimize the yaw angles of wind turbine rotors, such that the wakes are steered away from downwind turbines.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import foxes
import foxes.variables as FV
from iwopy.interfaces.pymoo import Optimizer_pymoo
from foxes_opt.problems import OptFarmVars
from foxes_opt.objectives import MaxFarmPower

/home/runner/work/foxes-opt/foxes-opt/.venv/lib/python3.10/site-packages/foxes/core/engine.py:4: TqdmExperimentalWarning: Using `tqdm.autonotebook.tqdm` in notebook mode. Use `tqdm.tqdm` instead to force console mode (e.g. in jupyter console)
  from tqdm.autonotebook import tqdm

Let’s create the foxes engine, which will be used for all calculations:

engine = foxes.Engine.new(
    "process",
    chunk_size_states=500,
    chunk_size_points=5000,
    verbosity=0,
)

In this example we are looking at a small 3 x 3 regualar wind farm with NREL5MW turbines:

farm = foxes.WindFarm()
foxes.input.farm_layout.add_grid(
    farm,
    xy_base=np.array([500.0, 500.0]),
    step_vectors=np.array([[1300.0, 0], [200, 600.0]]),
    steps=(3, 3),
    turbine_models=["opt_yawm", "yawm2yaw", "NREL5MW"],
    verbosity=0,
)

ax = foxes.output.FarmLayoutOutput(farm).get_figure()
plt.show()
plt.close(ax.get_figure())

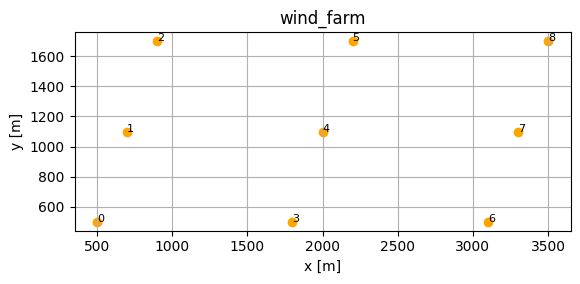
../_images/bbdc61de6174739ad282847a0bb954059a4ae56167b8630bb2625a1553a38768.png

Notice how the name of the optimization model opt_yawm, which will be defined shortly, appears in the list of turbine models. The idea is as follows:

First, the optimizer sets the FV.YAWM variable, representing yaw misalignment in degrees, i.e., a delta yaw value from greedy conditions
Then, the model yawm2yaw translates this into the absolute yaw value, i.e., the absolute turbine axis orientation, expressed in degrees
This setting is then used for thrust and power calculations, by the turbine type model NREL5MW.

We are considering sinlge-state uniform inflow conditions:

states = foxes.input.states.SingleStateStates(ws=9, wd=270, ti=0.06, rho=1.225)

The algorithm is defined next, including a TI wake model and the Bastankhah2016 wake model. Also notice the wake frame choice yawed, which realizes the wake bending for yawed conditions:

algo = foxes.algorithms.Downwind(
    farm,
    states,
    rotor_model="grid25",
    wake_models=["IECTI2019k_quadratic_ambka02", "Bastankhah2014_vector_ambka04"],
    wake_deflection="Jimenez",
    verbosity=0,
)

The optimization problem is power maximization by finding the optimal value of the variable FV.YAWM for each turbine:

problem = OptFarmVars("opt_yawm", algo)
problem.add_var(FV.YAWM, float, 0.0, -40.0, 40.0, level="turbine")
problem.add_objective(MaxFarmPower(problem))
problem.initialize()

Problem 'opt_yawm': Optimization variable list

        name   var   type  index    level  state  turbine  sel_turbine  init  \
0  YAWM_0000  YAWM  float      0  turbine     -1        0            0   0.0   
1  YAWM_0001  YAWM  float      1  turbine     -1        1            1   0.0   
2  YAWM_0002  YAWM  float      2  turbine     -1        2            2   0.0   
3  YAWM_0003  YAWM  float      3  turbine     -1        3            3   0.0   
4  YAWM_0004  YAWM  float      4  turbine     -1        4            4   0.0   
5  YAWM_0005  YAWM  float      5  turbine     -1        5            5   0.0   
6  YAWM_0006  YAWM  float      6  turbine     -1        6            6   0.0   
7  YAWM_0007  YAWM  float      7  turbine     -1        7            7   0.0   
8  YAWM_0008  YAWM  float      8  turbine     -1        8            8   0.0   

    min   max pre_rotor model_key  
0 -40.0  40.0     False  opt_yawm  
1 -40.0  40.0     False  opt_yawm  
2 -40.0  40.0     False  opt_yawm  
3 -40.0  40.0     False  opt_yawm  
4 -40.0  40.0     False  opt_yawm  
5 -40.0  40.0     False  opt_yawm  
6 -40.0  40.0     False  opt_yawm  
7 -40.0  40.0     False  opt_yawm  
8 -40.0  40.0     False  opt_yawm  

Problem 'opt_yawm' (OptFarmVars): Initializing
----------------------------------------------
  n_vars_int  : 0
  n_vars_float: 9
----------------------------------------------
  n_objectives: 1
  n_obj_cmptns: 1
----------------------------------------------
  n_constraints: 0
  n_con_cmptns: 0
----------------------------------------------

Next, we setup the solver:

solver = Optimizer_pymoo(
    problem,
    problem_pars=dict(vectorize=True),
    algo_pars=dict(type="GA", pop_size=100, seed=42),
    setup_pars=dict(),
    term_pars=("n_gen", 100),
)
solver.initialize()
solver.print_info()

Loading pymoo
pymoo successfully loaded
Initializing Optimizer_pymoo
Selecting sampling: float_random (FloatRandomSampling)
Selecting algorithm: GA (GA)

Problem:
--------
  vectorize: True

Algorithm:
----------
  type: GA
  pop_size: 100
  seed: 42

Termination:
------------
  n_gen: 100

Now everything is setup, and we can solve the problem:

with engine:
    results = solver.solve()
    solver.finalize(results)

=================================================
n_gen  |  n_eval  |     f_avg     |     f_min    
=================================================
     1 |      100 | -2.894092E-01 | -3.392528E-01

     2 |      200 | -3.139203E-01 | -3.392528E-01

     3 |      300 | -3.265914E-01 | -3.405948E-01

     4 |      400 | -3.346273E-01 | -3.584494E-01

     5 |      500 | -3.411709E-01 | -3.585472E-01

     6 |      600 | -3.461708E-01 | -3.585472E-01

     7 |      700 | -3.503315E-01 | -3.585472E-01

     8 |      800 | -3.535017E-01 | -3.585472E-01

     9 |      900 | -3.559392E-01 | -3.593399E-01

    10 |     1000 | -3.574720E-01 | -3.597935E-01

    11 |     1100 | -3.583098E-01 | -3.603311E-01

    12 |     1200 | -3.591337E-01 | -3.610024E-01

    13 |     1300 | -3.597703E-01 | -3.616003E-01

    14 |     1400 | -3.603916E-01 | -3.620144E-01

    15 |     1500 | -3.608891E-01 | -3.620728E-01

    16 |     1600 | -3.613228E-01 | -3.621632E-01

    17 |     1700 | -3.616381E-01 | -3.622094E-01

    18 |     1800 | -3.618580E-01 | -3.622279E-01

    19 |     1900 | -3.620020E-01 | -3.622863E-01

    20 |     2000 | -3.621277E-01 | -3.624825E-01

    21 |     2100 | -3.622280E-01 | -3.625173E-01

    22 |     2200 | -3.622978E-01 | -3.625173E-01

    23 |     2300 | -3.623588E-01 | -3.625494E-01

    24 |     2400 | -3.624133E-01 | -3.625519E-01

    25 |     2500 | -3.624545E-01 | -3.626254E-01

    26 |     2600 | -3.624911E-01 | -3.626301E-01

    27 |     2700 | -3.625166E-01 | -3.626301E-01

    28 |     2800 | -3.625482E-01 | -3.626493E-01

    29 |     2900 | -3.625685E-01 | -3.626493E-01

    30 |     3000 | -3.625929E-01 | -3.626493E-01

    31 |     3100 | -3.626097E-01 | -3.626493E-01

    32 |     3200 | -3.626247E-01 | -3.626709E-01

    33 |     3300 | -3.626336E-01 | -3.626709E-01

    34 |     3400 | -3.626413E-01 | -3.626709E-01

    35 |     3500 | -3.626480E-01 | -3.626769E-01

    36 |     3600 | -3.626546E-01 | -3.626769E-01

    37 |     3700 | -3.626597E-01 | -3.626769E-01

    38 |     3800 | -3.626639E-01 | -3.626773E-01

    39 |     3900 | -3.626671E-01 | -3.626773E-01

    40 |     4000 | -3.626711E-01 | -3.626795E-01

    41 |     4100 | -3.626739E-01 | -3.626809E-01

    42 |     4200 | -3.626760E-01 | -3.626830E-01

    43 |     4300 | -3.626778E-01 | -3.626835E-01

    44 |     4400 | -3.626791E-01 | -3.626850E-01

    45 |     4500 | -3.626801E-01 | -3.626850E-01

    46 |     4600 | -3.626813E-01 | -3.626875E-01

    47 |     4700 | -3.626825E-01 | -3.626875E-01

    48 |     4800 | -3.626838E-01 | -3.626877E-01

    49 |     4900 | -3.626849E-01 | -3.626877E-01

    50 |     5000 | -3.626859E-01 | -3.626891E-01

    51 |     5100 | -3.626868E-01 | -3.626918E-01

    52 |     5200 | -3.626878E-01 | -3.626922E-01

    53 |     5300 | -3.626888E-01 | -3.626925E-01

    54 |     5400 | -3.626900E-01 | -3.626954E-01

    55 |     5500 | -3.626913E-01 | -3.626954E-01

    56 |     5600 | -3.626922E-01 | -3.626954E-01

    57 |     5700 | -3.626932E-01 | -3.626956E-01

    58 |     5800 | -3.626941E-01 | -3.626956E-01

    59 |     5900 | -3.626946E-01 | -3.626956E-01

    60 |     6000 | -3.626949E-01 | -3.626957E-01

    61 |     6100 | -3.626951E-01 | -3.626957E-01

    62 |     6200 | -3.626953E-01 | -3.626957E-01

    63 |     6300 | -3.626955E-01 | -3.626959E-01

    64 |     6400 | -3.626956E-01 | -3.626959E-01

    65 |     6500 | -3.626956E-01 | -3.626959E-01

    66 |     6600 | -3.626957E-01 | -3.626959E-01

    67 |     6700 | -3.626957E-01 | -3.626959E-01

    68 |     6800 | -3.626958E-01 | -3.626960E-01

    69 |     6900 | -3.626958E-01 | -3.626960E-01

    70 |     7000 | -3.626959E-01 | -3.626960E-01

    71 |     7100 | -3.626959E-01 | -3.626960E-01

    72 |     7200 | -3.626960E-01 | -3.626966E-01

    73 |     7300 | -3.626960E-01 | -3.626966E-01

    74 |     7400 | -3.626960E-01 | -3.626966E-01

    75 |     7500 | -3.626961E-01 | -3.626966E-01

    76 |     7600 | -3.626961E-01 | -3.626967E-01

    77 |     7700 | -3.626962E-01 | -3.626967E-01

    78 |     7800 | -3.626963E-01 | -3.626967E-01

    79 |     7900 | -3.626964E-01 | -3.626967E-01

    80 |     8000 | -3.626966E-01 | -3.626967E-01

    81 |     8100 | -3.626966E-01 | -3.626967E-01

    82 |     8200 | -3.626967E-01 | -3.626967E-01

    83 |     8300 | -3.626967E-01 | -3.626967E-01

    84 |     8400 | -3.626967E-01 | -3.626967E-01

    85 |     8500 | -3.626967E-01 | -3.626967E-01

    86 |     8600 | -3.626967E-01 | -3.626967E-01

    87 |     8700 | -3.626967E-01 | -3.626967E-01

    88 |     8800 | -3.626967E-01 | -3.626967E-01

    89 |     8900 | -3.626967E-01 | -3.626967E-01

    90 |     9000 | -3.626967E-01 | -3.626967E-01

    91 |     9100 | -3.626967E-01 | -3.626968E-01

    92 |     9200 | -3.626967E-01 | -3.626968E-01

    93 |     9300 | -3.626967E-01 | -3.626968E-01

    94 |     9400 | -3.626967E-01 | -3.626968E-01

    95 |     9500 | -3.626967E-01 | -3.626968E-01

    96 |     9600 | -3.626967E-01 | -3.626968E-01

    97 |     9700 | -3.626968E-01 | -3.626968E-01

    98 |     9800 | -3.626968E-01 | -3.626968E-01

    99 |     9900 | -3.626968E-01 | -3.626968E-01

   100 |    10000 | -3.626968E-01 | -3.626968E-01

Optimizer_pymoo: Optimization run finished
  Success: True
  Best maximize_power = 16321.354958132983

print()
print(results)

fr = results.problem_results.to_dataframe()
fr[[FV.X, FV.Y, FV.AMB_WD, FV.YAWM, FV.TI, FV.REWS, FV.P]]

Results problem 'opt_yawm':
----------------------------
  Float variables:
    0: YAWM_0000 = 2.293505e+01
    1: YAWM_0001 = 1.476572e+01
    2: YAWM_0002 = 1.474903e+01
    3: YAWM_0003 = 1.088119e+01
    4: YAWM_0004 = 1.155909e+01
    5: YAWM_0005 = 1.152734e+01
    6: YAWM_0006 = -1.167784e+00
    7: YAWM_0007 = -1.122612e+00
    8: YAWM_0008 = -1.102372e+00
----------------------------
  Objectives:
    0: maximize_power = 1.632135e+04
----------------------------
  Success: True
----------------------------

		X	Y	AMB_WD	YAWM	TI	REWS	P
state	turbine
0	0	500.0	500.0	270.0	22.935052	0.060000	9.000000	2180.216367
	1	700.0	1100.0	270.0	14.765724	0.060000	8.702784	2160.960596
	2	900.0	1700.0	270.0	14.749031	0.060000	8.703452	2161.755846
	3	1800.0	500.0	270.0	10.881192	0.068637	8.010250	1724.208759
	4	2000.0	1100.0	270.0	11.559094	0.080826	7.734368	1558.379830
	5	2200.0	1700.0	270.0	11.527340	0.080863	7.734593	1558.825575
	6	3100.0	500.0	270.0	-1.167784	0.091396	7.942026	1736.645166
	7	3300.0	1100.0	270.0	-1.122612	0.092882	7.743524	1620.799686
	8	3500.0	1700.0	270.0	-1.102372	0.092974	7.741373	1619.563135

Finally, we can visualize the result by looking at the flow field:

with engine:
    o = foxes.output.FlowPlots2D(algo, results.problem_results)
    plot_data = o.get_mean_data_xy("WS", resolution=10, xmax=5000)

fig = o.get_mean_fig_xy(plot_data)
plt.show()

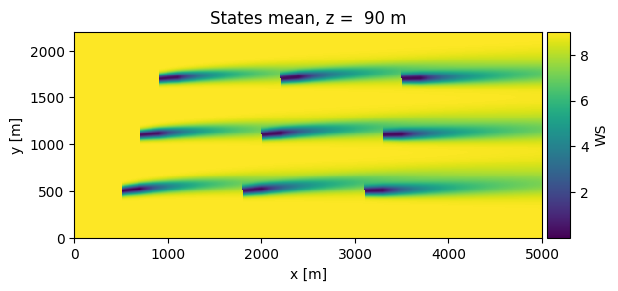
../_images/4825d8097969dc6d9df8baa1987ea4cba032343869928442431a34fb453f906d.png

Clearly the turbines are trying to avoid hitting downwind turbines with their wakes.