Turbine-based ambient flow data

In some cases the inflow data is directly known at the turbine locations, in terms of (state, turbine)-type data. Such data can be simulated with foxes by using the TurbinePointCloud states class, as demonstrated here.

We start by importing the necessary packages and setting up the engine:

%matplotlib inline
import numpy as np
from xarray import Dataset, date_range
import matplotlib.pyplot as plt

import foxes
import foxes.variables as FV

/home/runner/work/foxes/foxes/foxes/core/engine.py:4: TqdmExperimentalWarning: Using `tqdm.autonotebook.tqdm` in notebook mode. Use `tqdm.tqdm` instead to force console mode (e.g. in jupyter console)
  from tqdm.autonotebook import tqdm

engine = foxes.Engine.new("default", verbosity=0)

The first step is the creation of a regular grid of wind turbines:

n_turbines_x = 2
n_turbines_y = 3
n_turbines = n_turbines_x * n_turbines_y

farm = foxes.WindFarm()
foxes.input.farm_layout.add_grid(
    farm,
    xy_base=[1000, 1000],
    step_vectors=[[500, 0], [0, 500]],
    steps=[n_turbines_x, n_turbines_y],
    turbine_models=["DTU10MW"],
    verbosity=0,
)

o = foxes.output.FarmLayoutOutput(farm)
o.get_figure()
plt.show()
../_images/5cd154f5f961e9c99b4bcab74201fea0ea857dadb7f5ee017c3a10b5225daff7.png

Next, let’s create an artificial Dataset object that represents data with (time, turbine) dimensions, representing a timeseries in January 2026 measured at he turbines of the above wind farm:

n_times = 10
times = date_range("2026-01-01", periods=n_times, freq="10min", unit="s")
times

DatetimeIndex(['2026-01-01 00:00:00', '2026-01-01 00:10:00',
               '2026-01-01 00:20:00', '2026-01-01 00:30:00',
               '2026-01-01 00:40:00', '2026-01-01 00:50:00',
               '2026-01-01 01:00:00', '2026-01-01 01:10:00',
               '2026-01-01 01:20:00', '2026-01-01 01:30:00'],
              dtype='datetime64[s]', freq='10min')

np.random.seed(42)

# Turbine i has wind speed (10 + i.x) m/s, where x grows linear with time
ws = np.zeros((n_times, n_turbines))
ws[:] = 10 + np.arange(n_turbines)[None, :]
ws += np.linspace(0, 1, n_times, endpoint=False)[:, None]

# the wind directions are randomly selected from a southern sector:
wd = np.random.uniform(0, 190, (n_times, n_turbines))

sdata = Dataset(
    coords={"time": times},
    data_vars={
        "ws": (("time", "turbine"), ws),
        "wd": (("time", "turbine"), wd),
        "ti": ("time", 0.1 + np.arange(n_times) / 100),
        "rho": ("turbine", 1.2 + np.arange(n_turbines) / 100),
    },
)
sdata

<xarray.Dataset> Size: 1kB
Dimensions:  (time: 10, turbine: 6)
Coordinates:
  * time     (time) datetime64[s] 80B 2026-01-01 ... 2026-01-01T01:30:00
Dimensions without coordinates: turbine
Data variables:
    ws       (time, turbine) float64 480B 10.0 11.0 12.0 13.0 ... 13.9 14.9 15.9
    wd       (time, turbine) float64 480B 71.16 180.6 139.1 ... 8.593 61.81
    ti       (time) float64 80B 0.1 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19
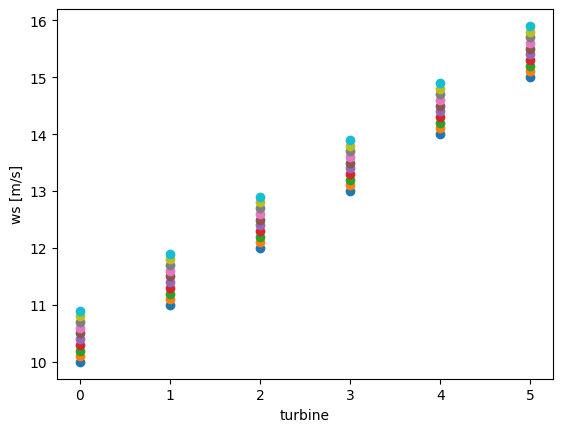
    rho      (turbine) float64 48B 1.2 1.21 1.22 1.23 1.24 1.25

This is what the wind speed per turbine looks like, increasing linearly with time as described above:

for t in range(0, n_times):
    plt.scatter(sdata["turbine"], sdata["ws"][t])
plt.xticks(sdata["turbine"])
plt.xlabel("turbine")
plt.ylabel("ws [m/s]")
plt.show()
../_images/d94da25f6483dddc809c9ca9fa456063e3355d28367a5090e131d127470a7fe8.png

The data frame sdata is the base for our ambient states object:

states = foxes.input.states.TurbinePointCloud(
    data_source=sdata,
    states_coord="time",
    turbine_coord="turbine",
    output_vars=[FV.WS, FV.WD, FV.TI, FV.RHO],
    var2ncvar={
        FV.WS: "ws",
        FV.WD: "wd",
        FV.TI: "ti",
        FV.RHO: "rho",
    },
)

Next, let’s create the algorithm object:

algo = foxes.algorithms.Downwind(
    farm=farm,
    states=states,
    wake_models=["TurbOPark"],
    rotor_model="centre",
)

We now run the farm calculation:

with engine:
    farm_results = algo.calc_farm()

Initializing model 'TurbinePointCloud'

Initializing algorithm 'Downwind'

------------------------------------------------------------
  Algorithm: Downwind
  Running Downwind: calc_farm
------------------------------------------------------------
  n_states : 10
  n_turbines: 6
------------------------------------------------------------
  states    : TurbinePointCloud()
  rotor     : CentreRotor()
  controller: BasicFarmController()
  wake frame: RotorWD()
  deflection: NoDeflection()
------------------------------------------------------------
  wakes:
    0) TurbOPark: TurbOParkWake(ws_quadratic, induction=Madsen, k=0.04*AMB_TI)
------------------------------------------------------------
  partial wakes:
    0) TurbOPark: axiwake6, PartialAxiwake(n=6)
------------------------------------------------------------
  turbine models:
    0) DTU10MW: PCtFile(D=178.3, H=119.0, P_nominal=10000.0, P_unit=kW, rho=1.225, var_ws_ct=REWS2, var_ws_P=REWS3)
------------------------------------------------------------


--------------------------------------------------
  Model oder
--------------------------------------------------
00) basic_ctrl
01) InitFarmData
02) centre
03) basic_ctrl
  03.0) Post-rotor: DTU10MW
04) SetAmbFarmResults
05) FarmWakesCalculation
06) ReorderFarmOutput
--------------------------------------------------


Input data:

 <xarray.Dataset> Size: 1kB
Dimensions:                  (state: 10, turbine: 6,
                              TurbinePointCloud_vars0: 2,
                              TurbinePointCloud_vars1: 1, tmodels: 1)
Coordinates:
  * state                    (state) datetime64[s] 80B 2026-01-01 ... 2026-01...
  * TurbinePointCloud_vars0  (TurbinePointCloud_vars0) <U2 16B 'WS' 'WD'
  * TurbinePointCloud_vars1  (TurbinePointCloud_vars1) <U2 8B 'TI'
  * tmodels                  (tmodels) <U7 28B 'DTU10MW'
Dimensions without coordinates: turbine
Data variables:
    TurbinePointCloud_data0  (state, turbine, TurbinePointCloud_vars0) float64 960B ...
    TurbinePointCloud_data1  (state, TurbinePointCloud_vars1) float64 80B 0.1...
    tmodel_sels              (state, turbine, tmodels) bool 60B True ... True 


Farm variables: AMB_CT, AMB_P, AMB_REWS, AMB_REWS2, AMB_REWS3, AMB_RHO, AMB_TI, AMB_WD, AMB_YAW, CT, D, H, P, REWS, REWS2, REWS3, RHO, TI, WD, X, Y, YAW, order, order_inv, order_ssel, weight

Output variables: AMB_CT, AMB_P, AMB_REWS, AMB_REWS2, AMB_REWS3, AMB_RHO, AMB_TI, AMB_WD, AMB_YAW, CT, D, H, P, REWS, REWS2, REWS3, RHO, TI, WD, X, Y, YAW, order, order_inv, order_ssel, weight
DefaultEngine: Selecting engine 'single'
SingleChunkEngine: Calculating 10 states for 6 turbines
SingleChunkEngine: Starting calculation using a single worker.
SingleChunkEngine: Completed all 1 chunks

The results demonstrate that all data was correctly passed from the flow states to ambient variables:

farm_results.to_dataframe()[
    [FV.AMB_WD, FV.AMB_RHO, FV.AMB_TI, FV.AMB_REWS, FV.REWS, FV.P]
]
AMB_WD AMB_RHO AMB_TI AMB_REWS REWS P
state turbine
2026-01-01 00:00:00 0 71.162623 1.20 0.10 10.0 8.870120 5203.170419
1 180.635718 1.21 0.10 11.0 10.952161 9691.624197
2 139.078849 1.22 0.10 12.0 8.375921 4343.136364
3 113.745112 1.23 0.10 13.0 13.000000 10648.334192
4 29.643542 1.24 0.10 14.0 14.000000 10639.821463
5 29.638959 1.25 0.10 15.0 15.000000 10679.230067
2026-01-01 00:10:00 0 11.035886 1.20 0.11 10.1 10.099999 7695.677599
1 164.573468 1.21 0.11 11.1 8.843683 5122.190590
2 114.211852 1.22 0.11 12.1 11.307228 10001.853148
3 134.533790 1.23 0.11 13.1 13.100000 10647.743528
4 3.911054 1.24 0.11 14.1 14.100000 10641.205377
5 184.282872 1.25 0.11 15.1 15.100000 10683.640267
2026-01-01 00:20:00 0 158.164102 1.20 0.12 10.2 10.016835 7493.719106
1 40.344431 1.21 0.12 11.2 11.197560 9927.517681
2 34.546744 1.22 0.12 12.2 11.338420 10031.238134
3 34.846857 1.23 0.12 13.2 13.200000 10646.824776
4 57.806026 1.24 0.12 14.2 14.200000 10645.627421
5 99.703722 1.25 0.12 15.2 15.200000 10679.614088
2026-01-01 00:30:00 0 82.069554 1.20 0.13 10.3 9.897905 7219.693837
1 55.333537 1.21 0.13 11.3 11.299817 10024.117128
2 116.252050 1.22 0.13 12.3 12.228169 10641.401600
3 26.503834 1.23 0.13 13.3 13.300000 10645.906025
4 55.507483 1.24 0.13 14.3 14.300000 10650.049446
5 69.608750 1.25 0.13 15.3 15.300000 10675.472075
2026-01-01 00:40:00 0 86.653297 1.20 0.14 10.4 8.815365 5116.000772
1 149.183433 1.21 0.14 11.4 11.344388 10066.222064
2 37.938019 1.22 0.14 12.4 12.398959 10643.009222
3 97.704543 1.23 0.14 13.4 13.230629 10646.543368
4 112.558768 1.24 0.14 14.4 13.468027 10644.695796
5 8.825578 1.25 0.14 15.4 15.400000 10671.330063
2026-01-01 00:50:00 0 115.433522 1.20 0.15 10.5 10.500000 8667.053105
1 32.399584 1.21 0.15 11.5 11.500000 10213.223952
2 12.359803 1.22 0.15 12.5 12.500000 10643.960300
3 180.288252 1.23 0.15 13.5 13.500000 10644.068521
4 183.470086 1.24 0.15 14.5 12.322961 10641.666860
5 153.595496 1.25 0.15 15.5 12.173622 10639.964027
2026-01-01 01:00:00 0 57.876616 1.20 0.16 10.6 8.886403 5229.093269
1 18.557702 1.21 0.16 11.6 11.600000 10307.691123
2 130.004275 1.22 0.16 12.6 11.252646 9950.431709
3 83.628974 1.23 0.16 13.6 13.568073 10643.443104
4 23.187265 1.24 0.16 14.6 14.600000 10663.315518
5 94.083613 1.25 0.16 15.6 15.600000 10663.046038
2026-01-01 01:10:00 0 6.533819 1.20 0.17 10.7 10.607070 8927.065036
1 172.770876 1.21 0.17 11.7 11.026436 9765.861911
2 49.168197 1.22 0.17 12.7 11.814770 10480.000112
3 125.879234 1.23 0.17 13.7 13.700000 10642.231018
4 59.225104 1.24 0.17 14.7 14.700000 10667.737542
5 98.812924 1.25 0.17 15.7 15.700000 10658.904025
2026-01-01 01:20:00 0 103.874953 1.20 0.18 10.8 10.800000 9395.583194
1 35.122347 1.21 0.18 11.8 11.548786 10259.310838
2 184.221079 1.22 0.18 12.8 12.251232 10641.618692
3 147.275236 1.23 0.18 13.8 13.800000 10641.312266
4 178.504799 1.24 0.18 14.8 14.799416 10672.133754
5 170.017197 1.25 0.18 15.8 14.137962 10641.212448
2026-01-01 01:30:00 0 113.600996 1.20 0.19 10.9 10.899155 9636.373977
1 175.156105 1.21 0.19 11.9 11.529127 10240.739089
2 16.813575 1.22 0.19 12.9 12.897184 10647.698920
3 37.236744 1.23 0.19 13.9 12.873414 10647.145895
4 8.593185 1.24 0.19 14.9 14.900000 10676.581590
5 61.812763 1.25 0.19 15.9 15.900000 10650.620000

For completeness, the states results at off-turbine evaluation points will be interpolated by point cloud methods.